In data analysis, the term Critical Constant Statistics is more than a buzzword—it's a framework that helps analysts extract predictable insights from noisy data by anchoring models to stable, interpretable constants. By design, Critical Constant Statistics emphasizes invariance, clarity, and replicable results, making it easier to explain findings to stakeholders and to validate results across datasets.
Overview of Critical Constant Statistics
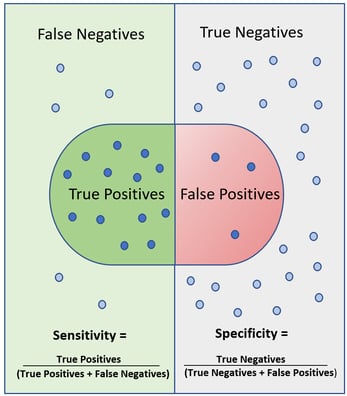
Critical Constant Statistics centers on the idea that certain values remain stable under a range of conditions. These constants act as anchors in models, guiding interpretation and reducing the volatility that often accompanies real-world data. For data analysts, this approach supports transparent feature engineering, clearer communication of results, and more reliable out-of-sample performance.
Key Points
- The constants provide invariants that help models generalize across shifts in data distribution.
- They simplify complex patterns into actionable, interpretable components for stakeholders.
- Estimating and validating constants can be integrated with cross-validation and backtesting workflows.
- Constant-based approaches reduce overfitting when data is noisy or sparse.
- Practical dashboards become more explainable when model behavior is described through stable constants.
Foundations and Why They Matter
At its core, Critical Constant Statistics identifies values that remain meaningful as data evolves. This stability enables analysts to distinguish genuine signals from transient noise, a distinction that becomes crucial when presenting results to non-technical audiences or when deploying models in changing environments. Emphasizing invariance, the approach supports reproducibility and scalable analytics across teams.
Implementing the Approach in Your Workflow
To apply Critical Constant Statistics, start by locating candidate invariants within your data—features or thresholds that do not shift dramatically under typical perturbations. Next, formalize these candidates as constants within your models, and test their impact using robust validation procedures. Always accompany numeric outputs with clear explanations that tie constants to business outcomes.
Tip: Treat constants as living components of a model, not immutable legends. Regularly re-evaluate them against new data while maintaining a clear audit trail for changes.
Practical Examples Across Domains
In finance, a volatility-adjusted constant can anchor risk models, ensuring that predictions remain stable even as market regimes change. In healthcare analytics, a fixed threshold derived from clinical guidelines can serve as a reliable decision boundary. In manufacturing, a constant related to sensor calibration can prevent drift from degrading predictive maintenance models. Across these cases, Critical Constant Statistics helps bridge statistical rigor with operational readability.
Best Practices and Common Pitfalls
Best practices include documenting the origin of each constant, validating with out-of-time samples, and combining constants with flexible modeling techniques to capture nonlinearities where appropriate. A common pitfall is over-constraining a model with too many rigid constants, which can suppress genuine signals. Balance invariance with adaptability, and use constant explanations to build trust with stakeholders.
How do I determine when a constant should be recalibrated?
+Track performance drift over time using held-out data and monitored business metrics. If accuracy, calibration, or decision rates deteriorate beyond a predefined tolerance, consider re-estimating or adjusting the constant. Maintain an audit trail that records the conditions under which recalibration was triggered.
Can Critical Constant Statistics be combined with nonlinear models?
+Yes. Constants can act as anchors or features that feed into nonlinear learners. They often improve interpretability when paired with tree-based methods or neural networks, acting as stable inputs that the model can rely on even when other features fluctuate.
What data scenarios benefit most from using Critical Constant Statistics?
+Datasets with regime changes, sensor data with calibration drift, or cross-domain data where distributions shift are prime candidates. Constants provide a stable reference point that helps models remain reliable when raw features are volatile.
How should I interpret results that use Critical Constant Statistics?
+Interpretation should connect the constant to a tangible outcome, such as a threshold, rate, or invariant that persists across conditions. Use clear visuals to show how predictions or decisions hinge on the constant, and relate shifts in performance to changes in the underlying data neighbors.
